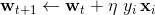Image: Graniers (Flickr / creative commons)
I had planned to write about something else, but the poor efficiency of the list-based Sudoku Solver keeps nagging me. I think I need to address that before venturing into other topics.
The list-based Sudoku Solver was my idea of the ”simplest-thing-that-could-work” outside or above the brute-force approaches. Since the board of the puzzle was maintained in a list of cells, all the access meant iterating through 81 elements and filtering what ever was needed, which added up to a lot of unnecessary work.
In the previous post, I sketched a couple of ideas for improvement. Although parallel computation might make things to happen faster, it does not make the approach any more efficient. I would prefer to tackle the problem with data structures and algorithms. Since my efforts at elegant tail-recursive solvers have remained inelegant, the list of improvements boils down to two: two-dimensional array for data structure and more elaborate pruning.
The array-based Sudoku board makes use of the array’s indexed positions when accessing cells, rows, columns etc. (see, the complete board class here).
case class ArrayBasedBoard(grid: Array[Array[Cell]]) {
override def cell(x: Int, y: Int): Cell = grid(y)(x)
override def row(y: Int): List[Cell] = grid(y).toList
override def col(x: Int): List[Cell] =
grid.map(r => r(x)).toList
...
The basic array in Scala is mutable as it is a representation of Java’s Array class. Although mutability goes against the grain of functional programming, I’ll make blatant use of it. For instance, when guessing, i.e., trying out a value for a cell from a set of candidates, I make copies of the board, and then assign the guessed values to the new grid. Copies of the board are needed as I might need to backtrack if the recursive iteration runs into a dead-end.
def +(c: Cell): ArrayBasedBoard = {
val newGrid = gridCopy
newGrid(c.y)(c.x) = c
ArrayBasedBoard(newGrid)
}
private def gridCopy: Array[Array[Cell]] = {
grid.map { row =>;
val newArray = new Array[Cell](row.size)
row.copyToArray(newArray)
newArray
}
}
I used the first 100 samples from University of Warwick‘s msk_009 dataset that contains mostly ”easy” puzzles as a quick touchstone. The data structure seemed to yield an improvement of about 20% in efficiency over the list-based approach — from 1300 ms to about 1000 ms.
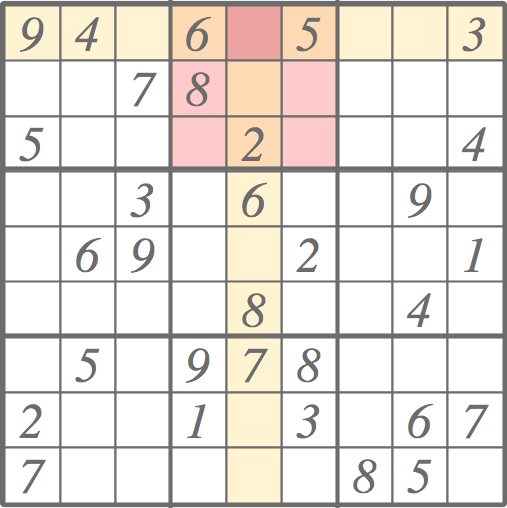
However, bigger improvement arose from the changes in pruning. In addition to pruning based on the neighboring values described in the previous post, the candidates of each cell can be pruned by neighboring candidates. Consider the puzzle below, for example. After eliminating the redundant candidates from each cell based on the initial values (large dark gray numbers), some cells have been solved (large light blue numbers), but this simple pruning cannot go any further. To proceed we would have to make a guess.
However, if the same pair of candidates occurs twice in the same row, column, or a block, that pair occur anywhere else on the same row, column, or a block, respectively. Making use of this rule, we can continue pruning and avoid guessing.
In the lower left corner, two cells with green background have candidate lists (small red numbers) identical comprising 2 and 3. Since 2 and 3 must to occur in those two cells, 2 and 3 cannot occur anywhere else in the given column. Thus, we can eliminate them from the candidate lists of the column. Since both cells occur also in the same bottom left 3 x 3 block, we can extend the pruning to the that block. The area of effect is colored with light blue.
There is another pair in top-right right corner: we have 4 and 6 in the same row and the same block. It can be used to prune cells that are colored in light yellow.
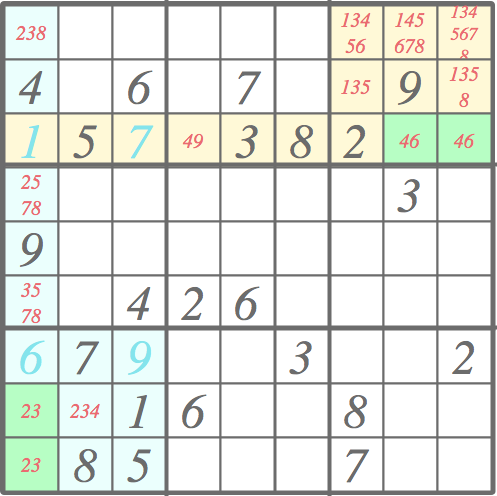
The pruning leads to the following outcome. Three further cells have been solved (green background) and the candidate lists in areas of effect have been pruned. As new cells have been resolved, the ”normal” pruning based on the neighboring values would pick up from here, followed by this kind candidate pair pruning, etc. Quite often, or should I say typically, the Sudoku puzzles in the newspapers can be solved with just pruning.
This sort of pruning with pairs elimination (see function eliminatePairs below) involves two phases: finding the pairs and pruning the candidate lists. The function twiceOccurringPairs is given the cells of a row, a column, or a block as a parameter, and it finds pairs of candidates that occur exactly twice. To this end, Scala provides quite elegant tools for manipulating lists.
def twiceOccurringPairs(cells: Traversable[Cell]): Set[Set[Int]] = {
cells.filter(_.cands.size == 2).
groupBy(_.cands).map(x =>; x._1 ->; x._2.size).
filter(_._2 == 2).map(_._1).toSet
}
def eliminatePairs(cells: Traversable[Cell]): List[Cell] = {
twiceOccurringPairs(cells).flatMap { pair =>
cells.collect {
case cell if (cell.value.isEmpty &&
cell.cands != pair &&
cell.cands.diff(pair) != cell.cands) =>
Cell(cell.x, cell.y, cell.cands.diff(pair))
}
}.toList
}
The elimination boils down to producing a list of cells for which the candidate list has been pruned. Again, the placement of those cells to the board exploits the mutability of the array.
eliminatePairs(board.col(y)).foreach { cell =>
board.grid(cell.y)(cell.x) = cell
}
Anyway, this pruning works for pairs of identical candidate lists. A similar rule would apply to identical triplets occurring thrice.
The presented pruning improves the efficiency considerably. Each elimination of a candidate pair means avoiding one guess, i.e., it eliminates one branch in the search tree. Using the 100 samples from msk_009 dataset, the pruning cuts the average processing time down to a third — from about 1000 ms to about 300 ms.
The situation is similar with the University of Warwick‘s data set of 95 hard Sudoku puzzles. The list-based solver spent about 51 seconds on the average, while the array-based solver with new pruning spends about 17 seconds on the average (67% improvement). The median time fell from about 5 seconds to 1 second (80% improvement).
The complete source can be found on GitHub.
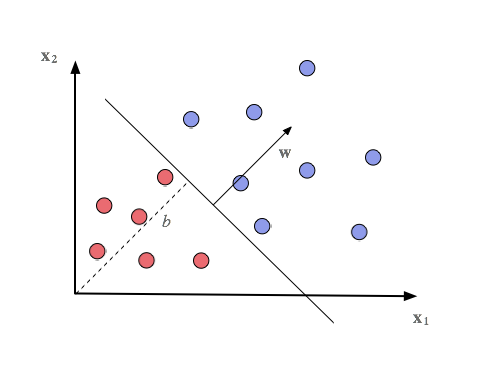The function f(x) measures the distance from a dot to the hyperplane. If the outcome is positive, the decision is yes, if zero or negative, no. All possible input signals (dots) are on one side of the hyperplane or on the other. That’s a dichotomy if there ever was one.
Untracked files 