Image: Neha Viswanathan (Flickr / creative commons)

I have worked out a quite few Sudoku puzzles on paper, but there has always been a sense of futility in the effort. It’s not that I’m against wasting time, but rather, instead of solving these Japanese numbers puzzles one-by-one, I have felt I should be working on a general solution, a program that can solve any Sudoku puzzle. I think the time has come to get this problem out of the way.

Sudoku is the perfect programming finger exercise: it has simple rules, there is not need for complicate data structures or need to integrate to external interfaces, and it involves no large amounts of data. You can attack it with brute force or try out something more elaborate. There may be regular competitions, I don’t know, but certainly it seems I am not alone: while I was looking for evaluation data, I noticed that Peter Norvig, among others, had posted a Sudoku solver apparently out of pretty much the same motives.

There is probably a wealth of Sudoku strategies and heuristics explained somewhere. Nevertheless, this time I am approaching the exercise with no background work. I’ll work out a simple Sudoku solver in Scala impromptu.

A Sudoku puzzle looks something like this: You have a 9-by-9 board or grid partitioned into 3-by-3 blocks with some numbers filled in. The purpose is to fill in the blanks with numbers from 1 to 9. The same number must occur exactly once in every row, in every column and in every 3-by-3 block.

With the general solution in mind, the first thing is to decide is how to represent the puzzle or the board. I’ve chosen the simplest structure that I could come up with: a list of individual cells (I’m hoping this will make the recursion easier). Each cell is defined by its coordinates and a set of candidate values, i.e., all values between 1 and 9 that are valid for the cell.

case class Cell(x: Int, y: Int, cands: Set[Int]) {
  def value: Option[Int] = {
    if (cands.size == 1)
      cands.headOption
    else
      None
  }
}

The board is a bit more elaborate. Since it is based on a list of cells, each access of rows, columns, or blocks requires a full scan of the 81 elements of in the list. This is the downside of simple data structure.

case class Board(cells: List[Cell]) {
  def row(y: Int): List[Cell] = {
    cells.filter(_.y == y)
  }
  def col(x: Int): List[Cell] = {
    cells.filter(_.x == x)
  }
  ...
}

The neighborhood of a cell consists of the row, the column and the block of the cell. In the board below, the neighborhood of the red cell is illustrated by yellow row and column together with pinkish block.

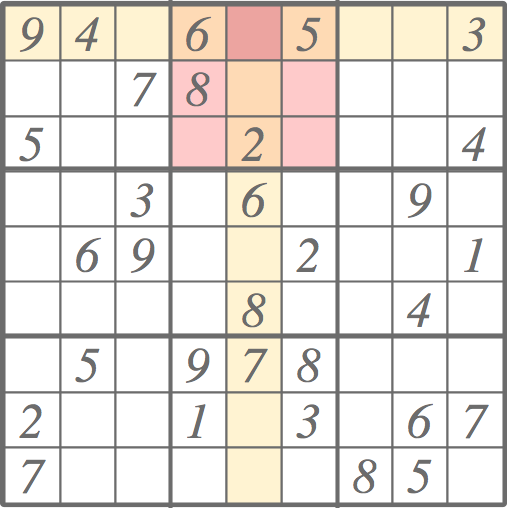
The idea is that by imposing the constraints, i.e., what neighboring cells already contain, we prune the list of candidates for each cell. In the example above, the list of possible values for the red cell cannot contain 2,3,4,5,7,8, or 9, which leaves us with only 1. And so on. When all the candidate lists are pruned down to one element, the puzzle is finished.

Sometimes, however, pruning is not enough, and we may have to guess. We try out one candidate for a cell and continue from there. Sometimes guesses result in dead-ends, and the board becomes inconsistent by having the same number twice in a row, a column or a block. In such a case, we have to back-track and guess again.

In my simple solver, prune is a tail-recursive function. It goes through all the cells eliminating the candidates based on the cell’s neighborhood. If pruning increases the number of resolved cells without producing any empty candidate lists, we prune further. If no improvement was attained or if pruning was too vigorous, return the board as is.

@tailrec
def prune(board: Board): Board = {
  val countBefore = board.cells.count(_.value.nonEmpty)
  val prunedCells: List[Cell] = board.cells.map { cell =>;
    val prunedCandidates = if (cell.value.nonEmpty)
      cell.cands
    else
      cell.cands.diff(board.neighborhood(cell.x, cell.y).
        flatMap(_.value))
    Cell(cell.x, cell.y, prunedCandidates)
  }
  val countAfter = prunedCells.count(_.value.nonEmpty)
  val empties = prunedCells.count(_.cands.isEmpty)
  if (countBefore < countAfter && empties == 0)
    prune(Board(prunedCells))
  else
    Board(prunedCells)
}

The actual iteration takes place in another recursive function iterate that receives a board as a parameter. If the board is invalid, for instance due to some cells pruned empty of candidates, we stop in failure. On the other hand, if the board contains a complete solution, we return that. Otherwise, we go through the unassigned cells (starting with the one with the shortest candidate list) and try out assigning candidates until we find a solution (or fail completely).

def iterate(board: Board): Option[Board] = {
  if (!board.isValid) {
    None
  } else if (board.isFinished) {
    Some(board)
  } else {
    prune(board).cells.filter(_.value.isEmpty).
      sortBy(_.cands.size).map { cell =>
      cell.cands.map { c =>
        val result = iterate(prune(board +
          Cell(cell.x, cell.y, Set[Int](c))))

        if (result.nonEmpty && result.get.isFinished)
          return result
      }
      return None
    }
    None
  }
}

I am not quite happy with this function. It is inelegant and certainly not tail-recursive. Nevertheless, it gets the job done. Let’s see how well.

The University of Warwick hosts datasets for the purpose of benchmarking automatic Sudoku solvers. Trying out their top95 data set of 95 hard Sudoku puzzles, my program yields an average response time of about 51 seconds with the median at 5 seconds and the maximum at friggin’ 15 minutes! It is faster than pen-and-paper approaches but it’s far from competitive. It is something of a consolation that all hard Sudokus were solved. Thus, the program works correctly, if sluggishly.

To improve the efficiency I could:

• replace the list-based representation of the board with a two-dimensional array for  faster access to cells, rows, and columns,
• adopt more effective pruning methods (e.g., if two cells on the same row/column have the same two candidates, those candidates can be eliminated from the rest of the neighborhood),
• parallellize the computation, and
• rewrite the iteration to a loop or a proper tail-recursive function.

And so, solving the initial problem of finding a general solution for Sudoku puzzles transforms into a new problem of finding a more efficient general solution. Sigh.

The source code (slightly refactored) can be found on GitHub.